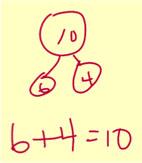
Here he was working with number bonds to consider the decomposition of 10 and then writing that as an equation. He gets a sense of the whole/part relationship pictorially and that moves to a sentence that communicates the relationship mathematically.
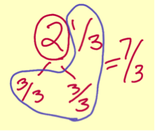

The more he works with 10 he develops a fluency that will help support his thinking. Now I am seeing him work through subtraction problems using his fluency with 10 to solve.

The problem was: Micah has 17 markers and gives 3 away.
What you see missing is a strategy to work with the 10. If he had ‘made 10’, not only would the work be more organized, he would be practicing the strategy of ‘completing a 10’ that is useful later on.
Not having a way to organize his work led to a mistake in his answer. This student didn’t organize his model and had to count and re-count his tally marks both when coming to the whole and after taking the 3 away. This led to a mistake in his ultimate answer.

He has also begun to “make 10” in his head in order to solve addition and subtraction problems such as (9+4 = 13) and (14 – 6 = 8). It is this kind of fluency with numbers that I wish I would have had the opportunity to practice using a variety of strategies.
The strategies used in The Story of Units have given both of my sons this very gift. Which makes me grateful...and a little bit jealous.
 RSS Feed
RSS Feed